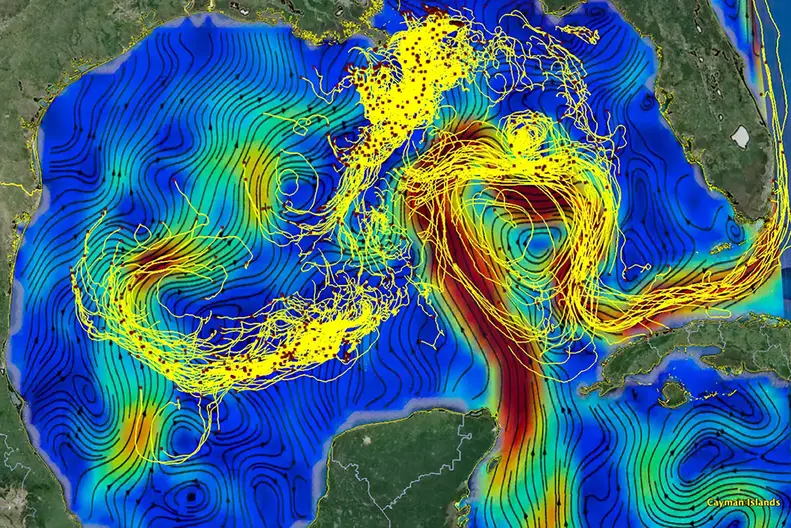
A new machine learning model makes more accurate predictions about ocean currents, which could help track plastic pollution and oil spills, as well as search and rescue. To study ocean currents, scientists release GPS-tagged buoys into the ocean and record their speed to reconstruct the currents that carried them. These buoy data are also used to detect “fits”, which are areas where water rises from the surface or sinks below the surface.

By accurately predicting currents and identifying inconsistencies, scientists can more accurately predict weather, predict approximately how oil will spread after a spill, or measure energy transfer in the ocean. A new model involving machine learning makes more accurate predictions than traditional models, according to a new study.

A multidisciplinary team of researchers, including MIT computer scientists and oceanographers, has discovered that the standard statistical model widely used for buoy data can be difficult to accurately reproduce currents or identify anomalies because it makes unrealistic assumptions about the behavior of water.

Researchers have developed a new model that incorporates information from fluid dynamics to better reflect the physics at work in ocean currents. They show that their method, which requires only a small additional computational cost, is more accurate than the traditional model at estimating currents and detecting inconsistencies.

This new model can help oceanographers make more accurate predictions based on buoy data, allowing them to more effectively monitor the transport of biomass (such as sargassum), carbon, plastic, oil and nutrients in the ocean. This information is also important for understanding and monitoring climate change.

“Our method captures the physical assumptions more accurately and precisely. In this case, we already know a lot of physics. We need this information so that the model can focus on learning about things that are important to us, such as what the currents from the buoys are or what this deviation is and where it occurs. “We feed you some of it.

Oceanographers use buoy velocity data to predict ocean currents and identify “differences” where water rises to the surface or sinks deeper.

To predict currents and detect inconsistencies, oceanographers used a machine learning technique known as the Gaussian process, which can make predictions even when little data is available. To perform well in this case, the Gaussian process must make assumptions about the data to generate an estimate.

The standard way of applying the Gaussian process to ocean data assumes that the latitude and longitude components of the current are uncorrelated. However, this assumption is not physically correct. For example, this current model assumes that current drift and eddy (eddy motion of the liquid) operate at the same magnitude and length scales. Broderick says oceanographers know that’s not true. The previous model also assumes that the frame of reference has a value, which means that the fluid will behave differently in the latitude and longitude directions.

“We thought we could solve these problems with a model that includes physics,” he says.

They created a new model that uses the so-called Helmholtz expansion to accurately represent the fluid dynamics principles. This method models the ocean current by separating it into an eddy component (capturing the eddy motion) and a diverging component (capturing the rise or fall of water). In this way, they provide the model with the basic physics information it uses to make more accurate predictions. This new model uses the same data as the old model. And while their method is more computationally intensive, the researchers show that the additional cost is relatively small.

high efficiency

They evaluated the new model using synthetic and real data from ocean buoys. Because the synthetic data is generated by the researchers, they can compare the model predictions with the actual flows and drifts available. But the simulations make assumptions that may not reflect real life, so the researchers also tested their models using data from real buoys floating in the Gulf of Mexico.

In all cases, their methods performed better for both tasks, current prediction and discrepancy detection, compared to a standard Gaussian process and another machine learning approach using a neural network. For example, in a simulation involving a whirlpool alongside an ocean current, the new method accurately predicted deflection while previous Gaussian process and neural network methods predicted deflection with very high confidence.

Broderick adds that the technique is also good for detecting eddies from a small set of floats.

Now that they have demonstrated the effectiveness of using the Helmholtz decomposition, the researchers want to add an element of time to their model, as currents can vary in both time and space. They also want to better capture how noise, such as wind, which sometimes affects buoy speed, affects data. Separating this noise from the data could make their approximation more accurate.

“We hope to take this noisy observed velocity field from the buoys and then tell what the real deflection and the real eddy are and predict the distance from those buoys, and we think our new technique will help with that,” he says.