Scientists from the universities of Paderborn and Leuven are solving a long-known problem in mathematics. Make history with the number 42: Scientists from the University of Paderborn and KU Leuven have solved a ten-year-old mathematical mystery called the ninth Dedekind number. Experts from all over the world have been searching for this value since 1991. Scientists from Paderborn arrived at the integer order with the help of the Noctua supercomputer located there. The results will be presented at the International Workshop on Boolean Functions and Applications (BFA) held in Norway in September.

The work of Lennart Van Geerthum, then a computer science student at KU Leuven and now a researcher at the University of Paderborn, began as a master’s thesis and turned into a huge success. Scientists join the elite group for their work: the first numbers in the series were found by mathematician Richard Dedekind himself when he described the problem in 1897, and later by great figures of early computer science such as Randolph Church and Morgan Ward. “For 32 years, calculating D(9) was an obvious challenge, and it was doubtful whether it would even be possible to calculate this number,” says Van Geerthum.

Dedekind number 8, the previous number in the Dedekind series, was found in 1991 using Cray 2, the most powerful supercomputer of the time. “It therefore seemed possible to us that it was already possible to calculate number 9 on a large supercomputer,” says Van Geerthum, explaining the motivation behind the ambitious project that he initially implemented with his master’s advisors. dissertation at KU Leuven.

Grains of sand, chess and supercomputers

The main subject of Dedekind numbers is functions called monotone Boolean functions. Van Hirtum explains: “Actually, a monotonous Boolean function of dimensions two, three, and infinite can be thought of as a game played with an n-dimensional cube. You balance the cube in one corner and then paint every remaining corner white or red. There is only one rule: Never white. you can’t place a corner over the red corner. This creates a kind of vertical red-white intersection. The object of the game is to count how many different segments there are. Their number is defined as the Dedekind number. Even if it doesn’t look like it, the numbers quickly become huge: Dedekind’s eighth number is already 23 stepped.”

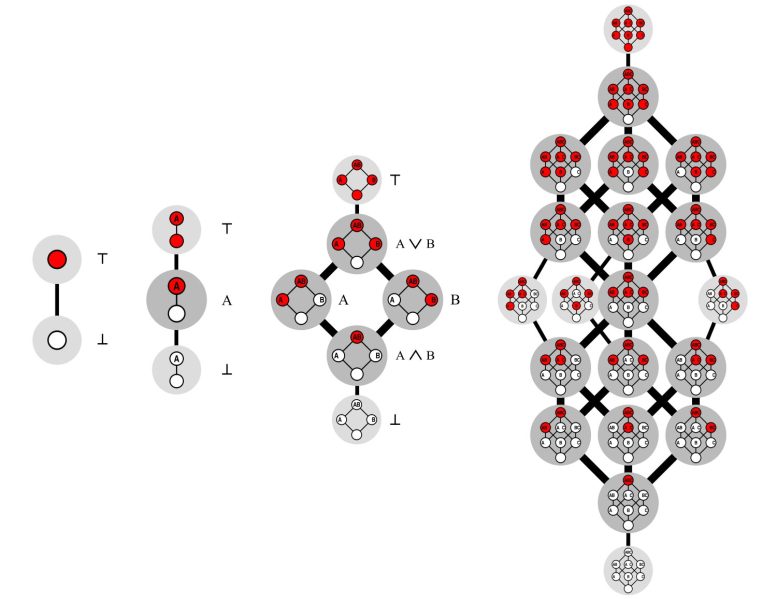
Figure 0 shows all possible cuts for sizes 1, 2 and 3. The number of times that these colored 2D, 3D, – N dimensional segments can be created is defined as the Dedekind number. Author: University of Paderborn

Relatively large – but incomparably easy to calculate – numbers are known from the legend of the invention of the game of chess. “According to this legend, the inventor of the game of chess asked the king as a reward for just a few grains of rice for each square of the chessboard: one for the first square, two for the second, four for the third . . . and twice as much in each of the squares below. , quickly realized that this demand could not be fulfilled, because there is not that much rice in the whole world. The number of rice grains on a full board would be 20 digits, which is an incredible number, but still less than D(8). Van Geerthum said: “Once you do it, it becomes clear that determining D(9) will require both a computationally efficient method and a very fast computer.”

To calculate D(9), the scientists used a technique known as the P-coefficient formula, developed by Patrick De Kausmaker, supervisor of the master’s thesis. It makes it possible to calculate Dedekind numbers not by counting but by a very large sum. This lets you decode D(8) in just eight minutes on a regular laptop. But what takes eight minutes for D(8) turns into hundreds of thousands of years for D(9). Van Geerthum notes that even if you use a large supercomputer specifically for this task, it still takes many years to complete the calculation. The main problem is that the number of members in this formula is growing incredibly fast. “In our case, we were able to reduce the number of terms to ‘only’ 5.5*10^18 using the symmetries in the formula – a huge number. For comparison, the number of grains of sand on Earth is about 7.5*10^18, which is to be underestimated. nothing, but 5.5*10^18 operations are quite possible for a modern supercomputer,” said the computer scientist. Problem: These terms are slow to compute on traditional CPUs, and currently using GPUs as the fastest hardware acceleration technology for many AI applications is inefficient for this algorithm.

Solution: Special hardware using highly specialized and parallel arithmetic devices called FPGAs (programmable gate arrays). Van Hirtum developed the first prototype of the hardware accelerator and began searching for a supercomputer that would have the necessary FPGA cards. Meanwhile, he got information about the Noctua 2 computer at the “Paderborn Parallel Computing Center (PC2)” at Paderborn University, which has one of the most powerful FPGA systems in the world.

PC2 President Professor Dr. Christian Plessl explains: “When Lennart Van Geerthum and Patrick De Koosmaeker contacted us, we knew immediately that we wanted to support the imaging project this month. Solving combinatorial problems with FPGAs is a promising field of application, and Noctua 2 is one of the few supercomputers in the world where experiments are even possible. “Extreme requirements for reliability and stability also challenge and test our infrastructure. The FPGA Expert Advisory Group worked closely with Lennart to adapt and optimize the application for our environment.” Source